Galileo starts out the third day with a general attack on the mindset people who do not wish to be confronted with facts that refute their a priori beliefs. (pp. 321-325)
Next, Galileo launches into a lengthy discussion of the supposed evidence that that the “two new stars” were sublunar. He uses a wealth of parallax calculations to disprove this notion and to show how a previous author had misused the same data to support the fallacy. (beginning on p. 326 and going to approx. p. 370.)
The gist of this is that a previous author (Chiaramonti) had collected the astronomical observations (meridian altitude) of the ‘new star’—nova—which appeared in Cassiopeia in 1572 taken by 13 individuals from different locations in Europe and North Africa. Taking any two of these observations, one can determine an estimate of the distance to the star/nova using parallax calculations. Chiaramonti chose 12 pairs of observations to use as his data set, from each of which he obtained a calculated distance to the star/nova that placed it somewhere within the assumed radius of the moon’s orbit, although the 12 values varied wildly within that range, some even being so small as to be less than the Earth’s radius—an obvious physical impossibility.
Galileo/Salviati takes the same data and demonstrates the fallacy propagated with it by Chiaramonti. He says that if one takes the remaining combinations of pairs of observations (of which there are a total of 78 possibilities), the vast majority of them place the star/nova well outside of the lunar orbit—thus, Chiaramonti selectively chose a subset of data to support his point instead of looking at all the data. Many of the remaining data pairs place the star/nova at an infinite distance (as far away as the fixed stars) due to observed directions to the star/nova from different points being parallel. And those data that placed the star/nova at a large, but finite, distance due to the convergence of the directional rays at a distant point could be interpreted to place it at an infinite distance (rays parallel) if it is assumed that the observations had small errors (amounting to a few minutes of arc), which is a highly reasonable assumption given the observational instruments of the time. Furthermore, some of the observations yield slightly diverging rays—which is a physical impossibility—thus supporting the assumption of small observational errors. But when these observations are again corrected for such errors, they also yield parallel rays—infinite distance. Thus, given the correspondence—within reasonable experimental error—of the vast majority of the data not used by Chiaramonti with a conclusion that the star/nova was in the realm of the fixed stars, it can be inferred that the data pairs which Chiaramonti chose are actually the ones with the grossest experimental errors. So at best, Chiaramonti was misguided. At worst, he purposely construed the data in a deceptive and self-serving way.
P. 371: The subject of the centrality of the earth in the universe is considered. The Aristotelian conception has the earth centered in a spherical universe. However, Galileo/Salviati observes that the entire spherical structure of the universe, as described by Aristotle, is predicated on one invalid assumption – the rotation of the universe. That is, because Aristotle assumed that the stars and other heavenly objects rotate around the earth—which is a reasonable conclusion to draw from casual observation and in the absence of other evidence—then he deduces from this that the universe must be spherical and finite since rotation is well-suited to spherical objects and infinite (or extremely large) objects can’t be thought to rotate. However, if this assumption—that the universe rotates—is denied, as Galileo claims based on more advanced observational evidence, then the whole system collapses and there is no need for the earth to be centered.
Another question that arises if the earth is considered to be the center of the universe about which all else revolves is, “why would the planets range sometimes farther and sometimes nearer from earth, as they are observed to do, if the earth is centered?” P. 374. Of course this problem is solved in a technical/mathematical way by the imposition of epicyclic motion on top of the orbital path, but there is no good satisfying explanation for why such epicyclic motion should occur. However, under a heliocentric view this apparent anomaly are quite naturally explained as not being an anomaly at all.
Starting on p 388, Galileo introduces three dilemmas for Copernican astronomy which purportedly troubled Copernicus himself because he could not explain them satisfactorily. These are (i) that Mars, though it appears to grow and shrink as would be expected by it’s changing distance from the earth as it orbits the sun, doesn’t appear to change in size nearly as much as would be expected quantitatively by the size of its orbit in a heliocentric model; (ii) Venus suffers the same argument as the previous one for Mars, plus it should show phases similar to the Moon since it has an orbit inside Earth’s, but it doesn’t appear to do so; and (iii) why should the Moon orbit the Earth if all other planets orbit the sun—what’s different about it? Galileo resolves these dilemmas in the following way.
The fact that Mars does not appear to the naked eye to change size nearly as much as predicted by a heliocentric model is simply an optical illusion caused by the distorting halo effect that afflicts the observation of all small points of light seen at a distance. The halo is an aura that surrounds the light that makes it look bigger than it actually is. However, the halo does not grow in proportion to the size of the light. Thus, for a large diameter light, the halo is hardly noticeable in effect, whereas for a small diameter light, the halo is proportionally very large and can make the light look several times its actual size. Thus, when one looks at Mars through a telescope, which enlarges the actual sphere without enlarging the halo, one sees the expected change in size over the course of its orbit. However, even without a telescope one can determine the accurate size of its disk by using an object of some small width at some distance in front of the observer to just obscure the disk—which will damp out the halo—and then measuring the angle subtended by the obscuring object (he used a string) measured back to the eye. Measuring the angle requires knowing the width of the object and the distance the eye must be from the object to just obscure the planetary disk. Galileo also notes that the distance measurement can be objected to on the grounds that the lens of the eye refracts the light and thus creates a virtual vertex which at a different location from the actual vertex. He describes a very ingenious way to estimate the distance correction due to this effect.
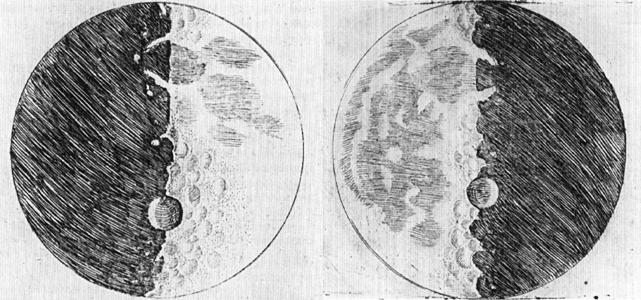
The same argument above also applies to resolve the size discrepancies of Venus. It also helps solve the problem of not observing the phases of Venus that should be apparent in a heliocentric model. The halo effect on the small point of light of Venus obscures any naked eye observation of its phases. However, when viewed through a telescope, which of course Copernicus didn’t have, Venus is enlarged sufficiently that the expected phases are quite apparent and are exactly what Copernican astronomy predicts.
Finally, with respect to the unique behavior of the Moon, the telescope again comes to the rescue. With the telescope, Galileo has observed ‘moons’ orbiting Jupiter and Saturn, and thus the Earth’s Moon is not unique at all but is rather a common structure in our solar system.
There is an interesting passage on p. 396, where Galileo/Salviati is discussing the motivations of Copernicus with respect to forwarding the heliocentric view. He says that Copernicus knew perfectly well that the Ptolemaic system of complicated systems of epicycles and equant points could be used to mathematically reconstruct the observed motion of the planets. But this was not very satisfying because each planet had to have different mathematical rules applied to it to work out its motion. Salviati says,
“Copernicus himself writes, in his first studies, of having rectified astronomical science upon the old Ptolemaic assumptions, and corrected the motions of the planets [by extending Ptolemaic reasoning] in such a way that the computations corresponded much better with the appearances, and vice versa. But this was still taking them separately, planet by planet. He goes on to say that when he wanted to put together the whole fabric from all individual constructions, there resulted a monstrous chimera composed of mutually disproportionate members, incompatible as a whole. Thus however well the astronomer might be satisfied merely as a calculator, there was no satisfaction and peace for the astronomer as a scientist. And since he very well understood that although the celestial appearances might be saved by means of assumptions essentially false in nature, it would be very much better if he could derive them from true suppositions…(thus) he began to examine under these two new suppositions [the annual and diurnal motions of the earth] the appearances and peculiarities of the planetary motions, all of which he had readily at hand. And seeing that the whole then corresponded to its parts with wonderful simplicity, he embraced this new arrangement, and in it he found peace of mind.”
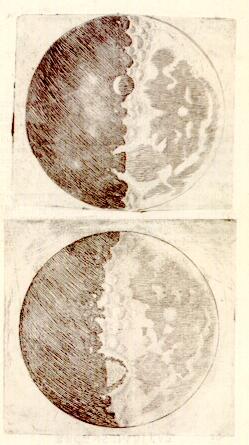
This is a classic illustration of what Thomas Kuhn called a “paradigm shift” in his seminal book The Structure of Scientific Revolutions (1962)—in fact, he uses just this example of Copernicus. According to Kuhn, at any given time, science operates within the bounds of a few major paradigms, which might be thought of as big picture theoretical frameworks—such as the geocentric Ptolemaic model. These paradigms tend to persist for a substantial length of time and to guide scientific thought and discovery (the Ptolemaic model persisted 2000 years!). However, over the lifetime of a paradigm, and in the routine course of scientific investigation, anomalies and discrepancies will begin to appear which seemingly cannot be explained or resolved within the framework of the paradigm. Perhaps many of these eventually do get resolved within the paradigm as better tools and techniques for observation are developed (a good example of this is Galileo’s use of the telescope to resolve the problem of why Mars appeared not to change in size sufficiently). Another way discrepancies are resolved is by modifying or extending the model—the development of epicycles to explain the retrograde motion of the planets is an example of such modifications of theory to accommodate anomalous behavior. Importantly, in Kuhn’s view, the desire to resolve all discrepancies within the framework of the current paradigm is very great because it is often the foundation of not only all scientific work and thought, but also perhaps of much cultural structure. If there are some anomalies that are persistent, these are typically set aside with the thought that they will be resolved eventually by one of the above means, or some other, when more is known. Thus, scientific paradigms always exist and operate with many discrepancies and anomalies extant, but this in itself does not detract from the validity and acceptance of the paradigm; rather, it is what typically fosters progress in the development, improvement, and explication of the paradigm.
Nonetheless, according to Kuhn, there will be two problems that will grow in the course of time. First, there will be some anomalies that will stubbornly resist resolution by either of the two means described above, or any other means for that matter, and these unresolved anomalies will begin to pile up. Second, the modifications to theory to account for other anomalies will begin to accumulate in such a way as to give the model an unwieldy and ad hoc character. At some point, therefore, a scientist or group of scientists will become so uncomfortable with the unresolved discrepancies and the increasingly contrived nature of the model that he/she/they will make a break from the accepted paradigm and propose a radical alternative—that is, they effect a paradigm shift. Of course, at first such a shift will be resisted by a scientific community invested in the previous paradigm, but over time, if the new paradigm consistently proves itself to be a more satisfactory explanation with fewer anomalies and more coherency, if will gain acceptance. Kuhn writes,
“…one source of crisis which confronted Copernicus was the mere length of time during which astronomers had wrestled unsuccessfully with the reduction of the residual discrepancies in Ptolemy’s system. When, for these reasons or others like them, an anomaly comes to seem more than just another puzzle of normal science, the transition to crisis and to extraordinary science has begun. The anomaly itself now comes to be more generally recognized as such by the profession. More and more attention is devoted to it by more and more of the field’s most eminent men. If it still continues to resist, as it usually does not, many of them may come to view its resolution as the subject matter of their discipline. For them the field will no longer look quite the same as it had earlier. Part of its different appearance results simply from the new fixation point of scientific scrutiny. An even more important source of change is the divergent nature of the numerous partial solutions that concerted attention to the problem has made available. The early attacks upon the resistant problem will have followed the paradigm rules quite closely. But with continuing resistance, more and more of the attacks upon it will have involved some minor or not so minor articulation of the paradigm, no two of them quite alike, each partially successful, but none sufficiently so to be accepted as paradigm by the group. Through this proliferation of divergent articulations (more and more frequently they will come to be described as ad hoc adjustments), the rules of normal science will become increasingly blurred.” p. 82.
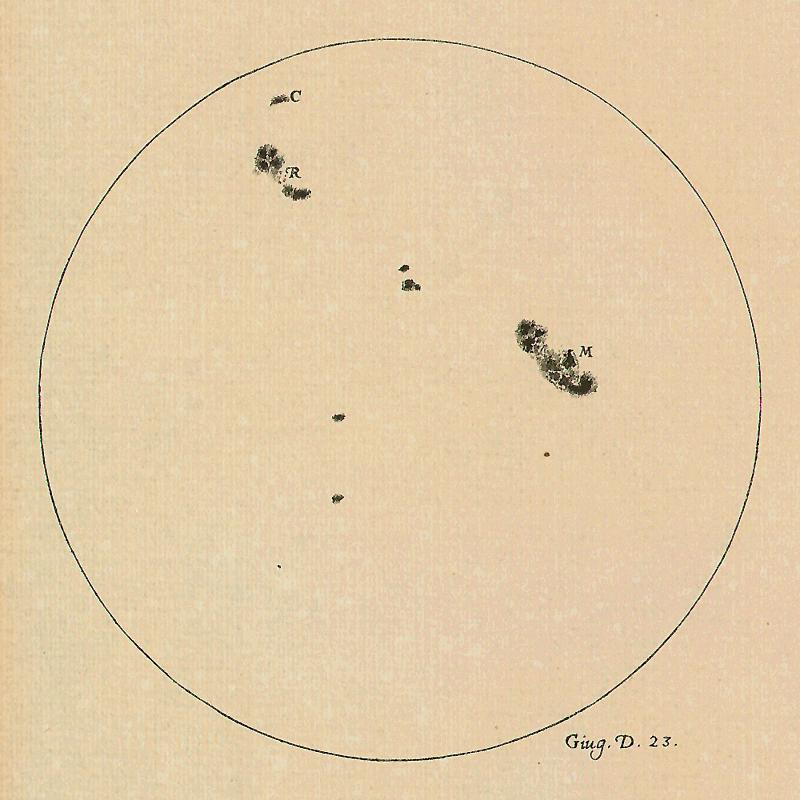
Beginning around page 402, Galileo/Salviati begins a discussion of an argument for the annual orbit of the earth about the sun which is very powerful and which is important in that is illustrates the Copernican/heliocentric model’s power not only to account for historically observed motions and phenomena, but also to predict future observations. This argument has to do with the tilt axis of sun, the revolution of the sun, and the resultant motion of sun spots. In observing sun spots with his telescope, Galileo notices them, at a given point in time, moving across the face of the sun along a straight line angled slightly downwards. This leads Galileo to hypothesize that the sun rotates about its own axis which must be tilted with respect to the plane of the ecliptic (the plane of the solar system). Furthermore, for the spots to be observed to move in a straight line angled down, the earth must be in one very particular location relative to the sun and its tilt axis. And if the earth is orbiting about the sun, then its position relative to the sun and its tilt axis will change during the course of the year, and consequently the nature of the path that the sun spots take across the face of the sun should be predictably different at different times of the year. At three month intervals, the same sun spot should be seen to cross the face of the sun along paths that are alternately (i) straight, angled down, (ii) curved, concave up, (iii) straight, angled up, and (iv) curved, concave down. This predicted behavior is just what Galileo observed! Galileo/Salviati says (on p. 410), “…after having given very careful thought to what might be said on this matter, we have not found under the ancient system any reply adequate to harmonize the course of the spots with human reason.” In other words, Galileo saw this as convincing evidence in support of the Copernican system.
Galileo uses this as a lead-in to a proposal for how to measure the heretofore unobserved parallax of the fixed stars which must exist if the earth has an annual orbit (i.e., if the earth is moving through space). He discusses the fact that such a parallax will be exceedingly small and will therefore require better methods of observation than currently exist. On page 449, Salviati says, “I wish you had said that if such a variation were perceived [stellar parallax], nothing would remain that could cast doubt upon the earth’s mobility, since no counter could be found to such an event. But even though this may not make itself visible to us, the earth’s mobility is not thereby excluded, nor its immobility necessarily proved.”
This is a good example again of what Kuhn was referring to with respect to anomalies. Assuming for a moment that the Copernican system was accepted as the new and proper paradigm, Galileo is admitting that the nonobservance of the stellar parallax is an anomaly for that system. But he is suggesting that it is an anomaly that will be resolved with improved observational capabilities. (In fact the stellar parallax is not observed until the 1830’s when Wilhelm Struve used a Fraunhofer telescope to look at the star Vega and a nearby, but much farther and dimmer, star. Galileo suggested this ‘double-star’ method of observing parallax, ~p. 447. He found that Vega's parallax amounted to about 1/8th second of arc (the diameter of a penny at twenty miles), the angle revealing Vega to be some 25 light years or 150 trillion miles away.)
This is a good point to bring in a little discussion of another (besides Kuhn) influential contribution to the philosophy of science. Karl Popper (1902-1994) proposed a very powerful conception of the nature of scientific investigation. Previous to Popper, science had been conceived primarily as a search for truth about the nature of the world. Science was assumed to progress by seeking evidence to confirm scientific theories or hypotheses—that is, by proving that various proposed pieces of the puzzle were true. Popper, on the other hand, argued that instead of science progressing by the verification of hypotheses, rather it progressed by a process of falsification. This thought arises from the proposition that no number of specific positive observations is ever sufficient to confirm a universal generalization. However, only one specific negative observation is sufficient to disconfirm or falsify a universal generalization. Thus scientific theories are never verified; they can only be corroborated or falsified. (This idea of falsification has come to be used as a test for whether or not a theory is truly scientific).
Specific notes for the "Third Day":
- Salviati asks Aristotle to choose, Brilliancy of Aristotle for his time.
- A main point for Galileo is that Aristotle was brilliant for his time even though he was wrong.
- 3 problems for Copernican Astronomy: no phases in venus, no change in venus, no phases of mars.
- Pointy edges of light on stars, all shining objects have a halo about them.
- Halo is the same size no matter what size the light is.
- Main task of astronomers is to give reasons for the appearances, Copernicus restored astronomy on Ptolemaic assumptions, Copernicus wasnt trying to prove Ptolemy wrong but tried to improve on the system for better measurements, Copernicus also saw the Ptolemaic system as a massive Chimera and in the course of trying to unravel it he comes upon the "sun in the center" system of astronomy.
- Ptolemaic was believed for about 2000 years making it a successful paradigm even though it was incorrect.
- Annomaly- Cant be explained by a paradigm.
- Sunspots was actually Galileos Great work.
Graphs of the "Third Day":