The first half of the second day is devoted to exploring in detail the arguments for and against the immobility of the earth as pertain to observations made on the earth. But first Galileo discusses the Copernican argument that it is simpler to revolve the earth than to revolve the immensity of the heavens. In addition, a 24 hr rotation of the stellar sphere is not consistent with the progressively longer periods of the planets the farther they are from us. Also, stars near poles would move in much smaller circles than those at the equator. Also, the stars near the poles change their motion, perhaps starting and stopping, with the equinoctial precession (the change in tilt direction of earth’s axis over long time.) Also, why wouldn’t earth be swept up in a heavenly rotation? Simplicio’s rebuttal: infinitely powerful mover can do anything.
Then, lowing his gaze to earthly observations, Galileo starts into a lengthy discussion of relative motion. In this vein, Simplicio lays out several Aristotelian arguments for the immobility of the earth:
If earth rotates, then

• An object falling from a height falls in a straight line and lands at a spot directly under where it was dropped from. If earth rotates, object should land at a spot to the west of where it was dropped.
• This ‘falling behind’ behavior is allegedly observed in an object dropped from the mast of a swiftly sailing ship.
• Similar arguments are made about a cannonball fired vertically upward.
• Cannon shots to the east and west should travel different distances—shorter to east, farther to west—because of the earth rotating while cannonball aloft.
• Cannon shots to the north and south should not go straight, but should veer west.
• Clouds and birds should be swept away to the west.
• Things on earth should be scattered about due to the centrifugal effect.

None of these things are observed, so earth must not rotate.
As an aside, Galileo makes an interesting observation about the nature of prior commitment on page 149:
“I commenced to believe that one who forsakes an opinion which he imbibed with his milk and which is supported by multitudes, to take up another that has few followers and is rejected by all the schools and that truly seems to be a gigantic paradox, must of necessity be moved, not to say compelled, by the most effective arguments.”
Galileo then levies arguments to diffuse each of the problems posed above. These arguments all stem from one basic premise: that the only motion of an object that an observer can sense is that motion which is relative between the two; that is, motion that the object has differently from the observer. In the case of the rotation of the earth, any earthbound observer will have the same rotational motion as the object observed, and hence that rotational motion will not be detectable by the observation of the objects motion. That is, the earthbound reference frame necessarily precludes any detection of the earth’s rotation by viewing other earthbound (including within atmosphere) objects.
Galileo casts this as a logical fallacy on the part of Aristotle. Consider the logical argument form,
If A, then B
A is observed
Therefore B,

Using this form, Aristotle is arguing,
If objects fall vertically toward the earth’s center, then the earth must not rotate.
That objects fall vertically toward the earth’s center is observed
Therefore, the earth must not rotate.

But Galileo says that the fallacy occurs in the second step. That is, our observation that objects fall vertically is corrupted by the possibility that we, as observers, are part of the same moving reference frame as the object we are observing, and hence the falling object—and us—might be moving in a thousand different ways that we are unaware of.

So in the case of an object dropped from a height, it not only accelerates downward, it also has a constant horizontal velocity equal to the velocity of the earth’s rotation. This latter is the part undetected because the observer also has this velocity. Therefore, while it apparently falls straight down, it is actually following an arc as illustrated below. But since an observer who is positioned, for example, at the same lateral position as the original position of the object, is traveling with the same horizontal velocity, then he/she does not notice the lateral component of the motion, only the vertical component.

One counter-argument that can be brought against this relative motion explanation from an Aristotelian viewpoint is that this assumes that the object, when released, will continue to have the same horizontal velocity as the earth. An Aristotelian might say that since, when released, no force is continuing to move the object along with the earth, it should no longer have a horizontal velocity—this argument stems from the notion that motion must always be sustained by a force. Galileo/Salviati’s response is that the ‘impressed motion’ is kept by an object which detaches from another moving object, and this impressed motion only diminishes with respect to impediments (such as air resistance and friction). For example, if a man riding a horse at a swift gallop drops a ball straight down, the ball will be seen to bounce and roll along the ground in the direction of the horse, only being slowed down by the roughness of the ground—and the smoother the ground, the longer the motion is continued. (p. 181).
This is part of a longer critique of the Aristotelian concept that the continued motion of a projectile, after it has left contact with the forcing body, is due to some impressed motion upon the air that, as the air rushes in to fill the void behind the object, continues to move the object along for some time until the motion finally dissipates. Galileo attacks this concept by showing its absurdity—that is, the air can actually only act as a resistance to motion rather than acting to sustain it. One argument is as follows (p. 175):
Which would be blown away in a strong wind: a heavy rock or a ball of cotton? The ball of cotton of course. Which can be thrown farther: a heavy rock or a ball of cotton? The rock can obviously be thrown farther. Then if the air was responsible for sustaining the motion of a projected object, why in the first case would the air have no effect on the heavy rock and in the second case propel it a great distance, while in the first case it carried the cotton away and in the second case it failed to deliver the cotton very far at all? This is contradictory according to the Aristotelian view. On the other hand, if the air is considered to produce a contrary force upon the object, then both cases are easily explained and are consistent with one another.
Getting back to the main argument, Galileo addresses the other cases in similar fashions: cannonballs shot east, west, north, south, or straight up.
Sagredo gives a ‘striking example’ concerning the non-detection of common motion (p. 199) He describes the case of a man drawing a sketch in the cabin of a boat going from Venice to Alexandretta. With respect to the man and paper, who are traveling with the pen on the boat, the tip of the pen completes the motions necessary to sketch houses, and trees, etc. But with respect to an observer fixed on land, the tip of the pen completes a very long arc with tiny wiggles along it.

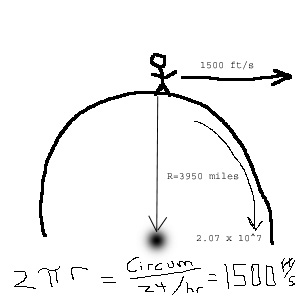
In the latter half of the second day, Galileo spends a great deal of time countering the argument that objects on the earth’s surface would be disrupted and flung off by the rotation of the earth (beginning at about p. 220). He begins by outlining the type of motion undergone by something cast off or projected as a result of circular or whirling motion, such as someone flinging a rock with the circular motion of a forked stick. He establishes that the object, upon leaving the propelling body, travels along a line tangent to the circle from which it left. It does not move radially away from the center. It moves along this tangent line with a uniform velocity equal to the velocity at the edge of the circular motion. However, when leaving earth, an object has a natural tendency due to gravity to fall back down toward the center of the earth. So the question really is, “does the velocity being cast off along a tangent line overpower the velocity of being drawn toward the center of the earth?” Galileo makes some detailed geometrical constructions to show that the power of gravity overrules the power of the circular motion to cast off object from the earth’s surface.

Specific points from the "Second Day":

• The beginning of the second day talks about the first day .
• Galileo deflects some of the heat from his book by pretending to present a neutral view of all of the subjects.
• People just accept Aristotle at face value, but Galileo decided to challenge that with evidence.
• If Aristotle could come back and use a telescope he would probablly change his mide about his view.
• Prophecies are generally vague to seem less erroneus.
• Things can only be disproven but never absolutlly proven.
• Scientific theories are always temporary untill proven wrong.
• Gravity acts upon every rock even though you cannot measure every rock in the universe.
• Things are not scientific unless you can test and prove things.
• Syllogism ----------> If A then B, We have A, Therefore B
• Specific argument about dropping a rock from the mast of a ship.
• Long argument about dropping stone or dropping cotton and which will go further because of wind.
• Air only resists motion, NOT powering something along.
• Friction gets a bad rap, and is needed everyday just to stay stuck tot he earth.
• Specific argument about firing a cannon and measuring the distance that the ball travelled however they talk about having to do the experiment many times because they dont think that there is a cannoneer accurate enough to get accurate results from only a few trials.
• If the earth were to speed up to a certain ammount we would be physically thrown from the Earth.

Graphs from the "Second Day":

[The First Day] [The Third Day]